Homework 3

Due: Friday, February 15, 2019
Points: 100

1. (30 points) The Ackermann function A(m, n) is a mathematical function of some importance in theoretical computer science. It is commonly defined as: Please write a program that requests two nonnegative integers and computes A(m, n). The program must continue to do so until the user types an end-of-file (that is, control-D). Your program should simply print the value. Here is an example (the input is in red):

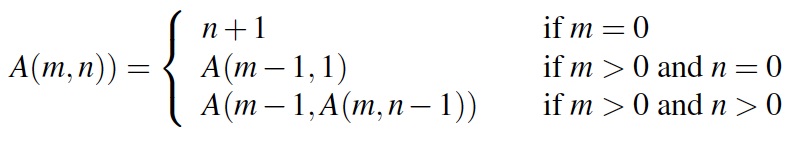
   Please enter a nonnegative integer: 2↵
   Please enter a nonnegative integer: 5↵
   13
   Please enter a nonnegative integer: control-D
   

   To type control-D, hold down the control key and type the D key. Nothing will appear visibly. Your program must stop if that is typed to either prompt.

   Please call your program “ack.py”.

2. (70 points) This program asks you to approximate a value of x for which x³ + ax² + bx + c = 0 using a technique called Newton’s method. This problem is adapted from the “Newton’s method for finding square roots” section of the textbook on p. 52.
   1. The algorithm for Newton’s method for computing a root of the expression x³ + 5x −3 is:
      1. Make an initial guess x₀ for the root (for example, take x₀ = 1)
      2. Use the following formula to compute successive x_ns until the desired accuracy is reached:
         x_n+1 = x_n − (x_n³ + ax_n² + bx_n + c) / (3x_n² + 2ax_n + b)

      Write a function called newton(a, b, c) to do this. Your function will take three integer arguments, namely a, b, and c. It should use Newton’s method to compute the approximation to a root of the above polynomial, to 10 decimal places.

      Hint: Remember, comparing floating point numbers is tricky! Rather than testing for equality of the previous guess with the new one, test that the difference between the two is 10⁻¹⁰.

   2. Write a program that calls your function. That program is to prompt the user for the 3 integer coefficients, and print both the approximate root root computed using Newton’s method (your function) and the absolute value of the difference between the value of the polynomial with that approximation and 0. Your output is to look like this (the input is in red):

      Enter the integer coefficient of x^2: 6↵
      Enter the integer coefficient of x: 11↵
      Enter the integer constant term: 6↵
      The approximate solution of x^3+6x^2+11x+6 is: -1.0000000000000002
      The error is 8.881784197001252e-16

      Your program is to read one set of coefficients and stop (that is, it should not loop and ask for another). Handle EOF and input errors properly, using try . . . except, and stopping on EOF or error.

      Here is some more sample output:

      Enter the integer coefficient of x^2: 0↵
      Enter the integer coefficient of x: 5↵
      Enter the integer constant term: -3↵
      The approximate solution of x^3+5x-3 is: 0.5640997330275644
      The error is 0.0

      Enter the integer coefficient of x^2: hello↵
      Coefficients must be integers

      Enter the integer coefficient of x^2: 4↵
      Enter the integer coefficient of x: control-D↵
      

      Your output is to be formatted as above; in particular, notice the polynomial in the output is to have no 0 coefficients (that is, if the coefficient of a term is 0, that term should not be printed), and if the coefficient is negative, it is to be preceded by a “−”, not a “+−”

   Please call your program “newton.py”.

Matt Bishop Office: 2209 Watershed Science Phone: +1 (530) 752-8060 Email: [email protected]

You can also obtain a PDF version of this. Version of February 6, 2019 at 12:29AM